Hits with Penalty

Choosing the Fitness Function

Hits with Penalty

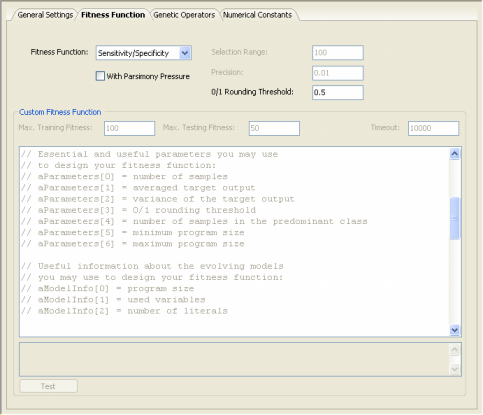
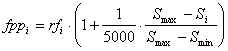GeneXproTools 4.0 implements the Hits with Penalty fitness function both with and without parsimony pressure. The version with parsimony pressure puts a little pressure on the size of the evolving solutions, allowing the discovery of more compact models.

For all classification problems, in order to be able to apply a particular fitness function, the learning algorithms of GeneXproTools 4.0 must convert the value returned by the evolved model into “1” or “0” using the 0/1 Rounding Threshold. If the value returned by the evolved model is equal to or greater than the rounding threshold, then the record is classified as “1”, “0” otherwise.

Thus, the 0/1 Rounding Threshold is an integral part of all fitness functions used for classification and must be appropriately set in the Settings Panel -> Fitness Function Tab.

The Hits with Penalty fitness function is very simple and highly efficient, and is based on the number of samples correctly classified.

More formally, the fitness f_i of an individual program corresponds to the number of hits and is evaluated by the formula:

If (TP_i = 0 OR TN_i = 0), then f_i = TP_i + TN_i; else f_i = 0

where TP_i is the number of true positives and TN_i is the number of true negatives.

So, for this fitness function, maximum fitness f_max is given by:

f_max = n

where n is the number of fitness cases.

Its counterpart with parsimony pressure, uses this fitness measure f_i as raw fitness rf_i and complements it with a parsimony term.

Thus, in this case, raw maximum fitness rf_max = n. And the overall fitness fpp_i (that is, fitness with parsimony pressure) is evaluated by the formula:

where S_i is the size of the program, S_max and S_min represent, respectively, maximum and minimum program sizes and are evaluated by the formulas:

S_max = G (h + t)

S_min = G

where G is the number of genes, and h and t are the head and tail sizes (note that, for simplicity, the linking function was not taken into account). Thus, when rf_i = rf_max and S_i = S_min (highly improbable, though, as this can only happen for very simple functions as this means that all the sub-ETs are composed of just one node), fpp_i = fpp_max, with fpp_max evaluated by the formula:

Home | Contents | Previous | Next