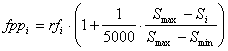| GeneXproTools 4.0 implements the Relative Error With Selection Range
(Relative with SR) fitness function both with and without parsimony
pressure. The version with
parsimony pressure puts a little pressure on the size of the
evolving solutions, allowing the discovery of more compact models. The Relative with SR fitness function explores the idea of a selection range and a precision. The selection range is used as a limit for selection to operate, above which the performance of a program on a particular fitness case contributes nothing to its fitness. And the precision is the limit for improvement, as it allows the fine-tuning of the evolved solutions as accurately as possible. Mathematically, the fitness fi of an individual program i is expressed by the equation:
where R is the selection range, P(ij) the value predicted by the individual program
i for fitness case j (out of n fitness cases) and
Tj is the target value for fitness case j. Note that the absolute value term corresponds to the
relative error. This term is what is called the
precision and if the error is smaller than or equal to the
precision then the error becomes zero. Thus, for a good match the
absolute value term is zero and fi
= fmax = nR.
where Si is the size of the program, Smax and Smin represent, respectively, maximum and minimum program sizes and are evaluated by the formulas: Smax = G (h + t) Smin = G where G is the number of genes, and h and t are the head and tail sizes (note that, for simplicity, the linking function was not taken into account). Thus, when rfi = rfmax and Si = Smin (highly improbable, though, as this can only happen for very simple functions as this means that all the sub-ETs are composed of just one node), fppi = fppmax, with fppmax evaluated by the formula:
|