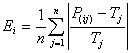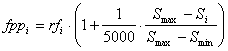| GeneXproTools 4.0 implements the Mean Absolute Error
(rMAE, with the small "r" indicating that it is based on
the relative error rather than the absolute) fitness function both with and without parsimony pressure. The
version with parsimony
pressure puts a little pressure on the size of the evolving
solutions, allowing the discovery of more compact models. The rMAE fitness function of GeneXproTools is, as expected, based on the standard mean absolute error, which is usually based on the absolute error, but obviously the relative error can also be used in order to create a slightly different fitness measure. The rMAE Ei of an individual program i is evaluated by the equation:
where P(ij) is the value predicted by the individual program
i for fitness case j (out of n fitness cases); and
Tj is the target value for fitness case j.
which obviously ranges from 0 to 1000, with 1000 corresponding to the ideal (the coefficient 1000 allows a fairer distribution of fitnesses for selection).
where Si is the size of the program, Smax and Smin represent, respectively, maximum and minimum program sizes and are evaluated by the formulas: Smax = G (h + t) Smin = G where G is the number of genes, and h and t are the head and tail sizes (note that, for simplicity, the linking function was not taken into account). Thus, when rfi = rfmax and Si = Smin (highly improbable, though, as this can only happen for very simple functions as this means that all the sub-ETs are composed of just one node), fppi = fppmax, with fppmax evaluated by the formula:
|