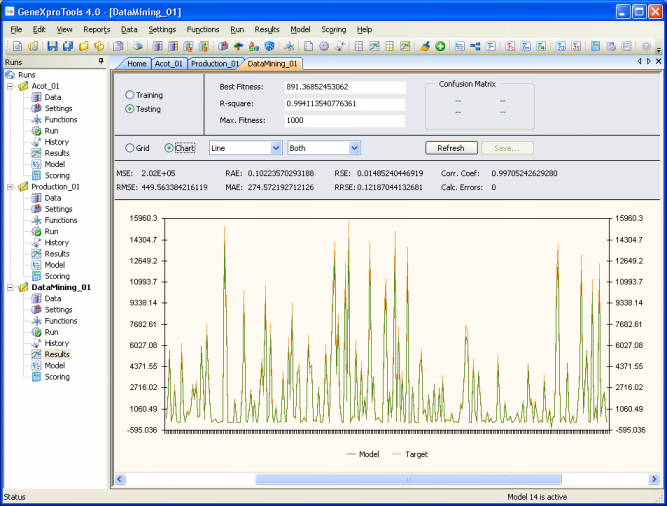
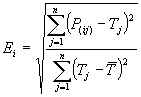|
The root relative squared error is relative to what it would have been if a simple predictor had been used. More specifically, this simple predictor is just the average of the actual values. Thus, the relative squared error takes the total squared error and normalizes it by dividing by the total squared error of the simple predictor.
By taking the square root of the relative squared error one reduces the error to the same dimensions as the quantity being predicted. Mathematically, the root relative squared error Ei of an individual program i is evaluated by the equation:
where P(ij) is the value predicted by
the individual program i for sample case j (out of n
sample cases); Tj is the target value for sample case
j; and
For a perfect fit, the numerator is equal to 0 and Ei
= 0. So, the Ei index ranges from 0 to infinity, with 0
corresponding to the ideal.
|
is
given by the formula:
